Criada por René Descartes (em latim Renatus Cartesius), filósofo e matemático francês e por Pierre de Fermat, matemático francês, a geometria analítica é uma importante ferramenta da pesquisa matemática, pois ela permite uma frutífera associação de dois dos seus grandes campos de estudo: a geometria e a álgebra. Com isso, abre-se os caminhos para estudar diversos entes geométricos, reproduzidos a partir de sua expressão algébrica, para enfim chegar às inferências matemáticas pretendidas.
Plano Cartesiano
Na geometria analítica, trabalha-se com um sistema de eixos perpendiculares com coordenadas chamados de plano cartesiano. Com este sistema de localização, podemos encontrar qualquer ponto que se queira, sem possibilidade de contradição, pois cada uma das coordenadas cartesianas corresponde a um e somente um ponto no plano cartesiano.
Observe o esquema de um plano cartesiano:
Assim, o plano cartesiano é formado pelos eixos x e y, chamamos respectivamente de eixos das abscissas e das ordenadas. O ponto (0,0) chamado de origem é o ponto de intersecção dos eixos.
Para localizar, por exemplo, os pontos A(2,3), B(-3,4), C(-2,-2) e D(1,-4), temos:
Distância entre dois pontos
Em geometria analitica, para encontrarmos a distancia entre dois pontos quaisquer, utilizamos dentro da geometria plana da mais conhecida relação métrica no triangulo retângulo: o teorema de Pitágoras.
Observe:
Como se trata de um triângulo retângulo, podemos utilizar o teorema de Pitágoras:
Assim, qualquer que seja a posição dos pontos A e B, podemos descobrir a distância entre eles através da fórmula supracitada.
Ex.: Prove que um triângulo com vértices A(0,5), B(3,-2) e C(-3,-2) é isósceles.
Triangulo isósceles é aquele que tem dois lados de medidas iguais. Então:
Como dAB = dAC e dAB é diferente de dBC , o triangulo é isósceles.
Ex.: Num triângulo ABC, sendo A(4,3), B(0,3), C um ponto do eixo das abcissas e AB=AC, determine C.
Como C está no eixo das abcissas, temos que C(x,0). Além disso, o segmento AB é igual ao segmento AC. Então:
dAB = dAC
Portanto, C(2,0).
Condição de alinhamento de três pontos
Dizemos que três pontos distintos estão alinhados, quando existe uma reta r que passa por estes três pontos. Em geometria analítica, descobrimos se os três pontos quaisquer A (d,e), B(f,g) e C(h,i) estão alinhados, quando o determinante da matriz formada pelas coordenadas destes pontos for igual a 0.
Observe:
O que implica na seguinte equação: dg + eh + fi – hg – id – fe = 0
Ex.: Determine o ponto C, sabendo que ele pertence ao eixo das ordenadas e está alinhado com A(3,2) B(5,4).
Do fato do ponto C está no eixo das ordenadas, temos que C(0,y).
Daí, temos:
3x4x1 + 2x1x0 + 1x5xy – 0x4x1 – yx1x3 – 1x5x2 = 0
12 + 5y -3y -10 = 0
2y + 2 =0
y = -1
Portanto, C(0,-1)
Ex.: Sabendo que P(a,b), A(0,3) e B(1,0) estão alinhados e P, C(1,2) e D(0,1) também são alinhados, determine as coordenadas de P.
ax3x1 + bx1x1 + 1x0x0 – 1x3x1 – 0x1xa – 1x0xb = 0
3a + b – 3 = 0
3a + b = 3
ax2x1 + bx1x0 + 1x1x1 – 0x2x1 – 1x1xa – 1x1xb = 0
2a + 1 – a – b = 0
b = a + 1
Substituindo a expressão resultante do segundo determinante, na expressão do primeiro determinante, temos:
Equação geral da reta
Na geometria euclidiana, dois pontos definem uma reta. Na geometria analítica, conhecendo as coordenadas de dois pontos A e B na reta r e a noção de condições de alinhamento de três pontos distintos, podemos determinar uma equação geral desta reta r.
Ex.: Qual é a equação geral da reta que passa pelos pontos A(1,4) e B(2,3)?
Vamos utilizar o ponto P(a,b) pertencente a reta r.
ax4x1 + bx1x2 + 1x1x3 – 2x4x1 – 3x1xa – 1x1xb = 0
4a+ 2b +3 – 8 – 3a – b = 0
a – b – 5 = 0
Assim, encontrando a equação geral da reta, podemos verificar se um ponto pertence ou não a esta determinada reta. Pois, se o ponto pertence a reta a igualdade se mantém. No caso da equação geral a – b – 5 = 0, temos que o ponto C(10,5) pertencem a reta, já o ponto D(3,-1) não pertencem. Vejamos:
Referências Bibliográficas.
DANTE, Luiz Roberto.Matemática: Ensino Médio. São Paulo: Ática, 2004.336p. V.3.
SANTOS, Carlos Alberto Marcondes dos; GENTIL, Nelson; GRECO, Sérgio Emílio. Matemática.São Paulo: Ática, 2000. 423p. (série novo ensino médio).






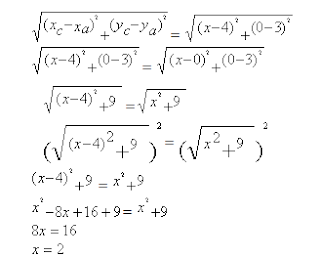







Nenhum comentário:
Postar um comentário